Deriving the Ideal Rocket Equation
Derivation (acceleration method)
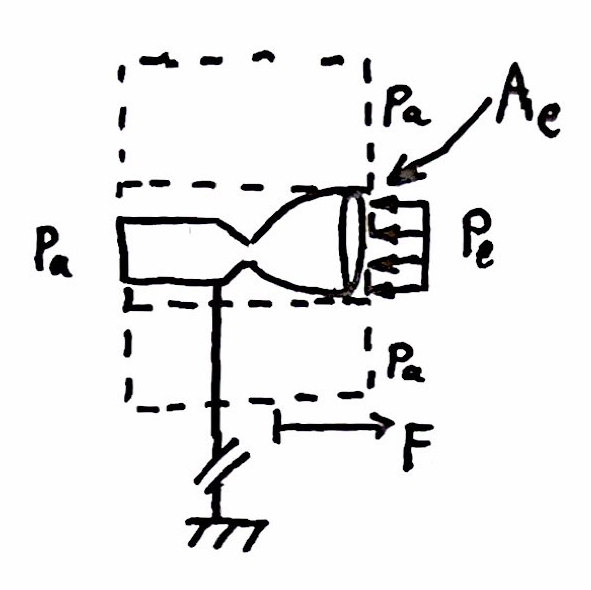
Control volume diagram of rocket engine
Conservation of linear momentum in a control volume:
$$\frac{\partial}{\partial t}\int_{CV} \rho \vec v dV = -\int_{CS}\rho v_{rel} \left(\vec v \cdot \vec{dA}\right) - \int_{CS} P\cdot\vec{dA} + \int_{CV}\rho\vec F dV + \Sigma\vec F$$
Steady state steady flow; no body forces:
$$\int_{CS}\rho v\cdot v\cos 0 dA = \Sigma F-\int_{CS}P\cdot \vec{dA}$$
Resolve accumulation and pressure terms:
$$\rho v_e^2 A_e = \Sigma F - (P_e-P_a)A_e$$
$$\dot m=\rho v A$$
Solve for thrust; substitute equivalent velocity:
$$\Sigma F = \dot m v_e + A_e (P_e-P_a)$$
$$v_{eq}=v_e+\frac{A_e(P_e-P_a)}{\dot m}$$
Thrust equation (\(v_e = v_{eq}\) at optimum expansion \(P_e=P_a\)):
$$T=\dot m v_{eq}$$
Apply Newton’s 2nd law:
$$T=m_v(t)a$$
$$m_v (t) = \text{Rocket Mass}$$
$$a = \frac{dv}{dt}$$
Define vehicle mass derivative from flow rate and burn time:
$$a=\frac{dv}{dt}=\frac{\dot m v_{eq}}{m_v(t)}$$
$$\dot m=\frac{m_p}{t_b}=\frac{dm}{dt}= -\frac{dm_v}{dt}$$
Separate variables:
$$\frac{dv}{dt}=\frac{-dm_v}{dt}\frac{v_{eq}}{m_v}$$
Integrate (equivalent velocity constant):
$$\int_{v_0}^v dv = -v_{eq}\int_{m_0}^{m_f}\frac{dm_v}{m_v}$$
Evaluate at limits:
$$v|^v_{v_0=0} = -v_{eq}\ln m_v|^{m_f}_{m_o}$$
$$\Delta v = v_{eq}[\ln m_0 - \ln m_f]$$
Final forms (equivalent velocity and specific impulse):
$$\Delta v = v_{eq}\ln\frac{m_0}{m_f}$$
$$\Delta v = I_{sp} g_0\ln\frac{m_0}{m_f}$$
$$I_{sp} = \frac{T}{\dot m g_0} = \frac{v_{eq}}{g_0}$$
Exponential form:
$$m_0 = m_f e^\frac{\Delta v}{I_{sp}g_0}$$
Fresh ink; it turned out perfect and looks even better healed. Done by Abe at Selfcare Trifecta
Last modified: 2025-06-19