Approximating π and the Circumference of the Universe on a Business Card

Note: this article was revised in Revisiting the “Pi Business Card”

Warning: my calculus and programming skills are pretty amateurish. Experts, try not to cringe

I saw a reddit comment claiming you can calculate π using a circle, and immediately had three thoughts:

That’s freaking awesome
It’s probably a bad thing that I don’t know how to do that
That would be awesome on the back of a business card

So, I started banging rocks together with a calculator until I figured out the equations.

Where does π come from?

For the uninitiated, π is just the ratio between a circle’s diameter and circumference. If you laid a 1 foot wide circle of string on the floor, that piece of string would be 3.14 feet long. In other words, its circumference is equal to π times the diameter: $c=2\pi r$. There are plenty of efficient formulas to calculate the value of π, but it’s difficult to understand why they converge to π as a naïve student.

Area of a circle and π

The area of a circle is π times the radius squared: $A=\pi r^2$. If the radius of the circle is $r=1$, its area is π. If I want to solve for the value of π, all I need to do is find the area of the $r=1$ circle using another method, and the answer is π! ($A=\pi$)

A circle is defined by the equation $x^2+y^2=r^2$, and half the circle is $y=\sqrt{r^2-x^2}$.

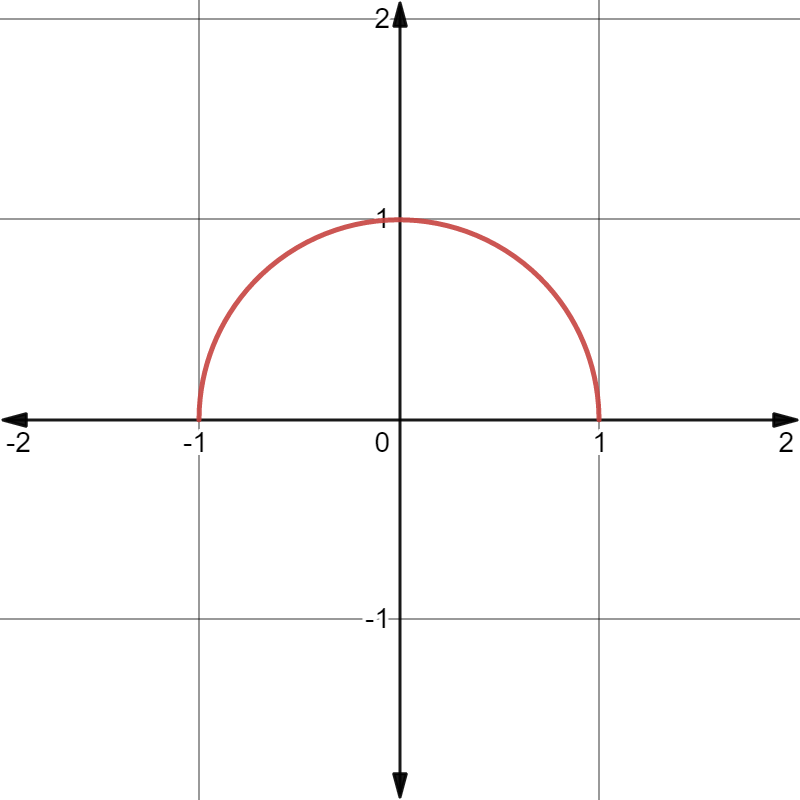
Graph of half a circle — Graph of $y=\sqrt{r^2-x^2},r=1$

Now that half of the circle is represented as a function of x, it’s possible to find the area underneath that curve by taking the definite integral of the function. The integral of the function between 0 and 1 is really the area of 1/4 the circle (represented by the purple shaded region in the graph below).

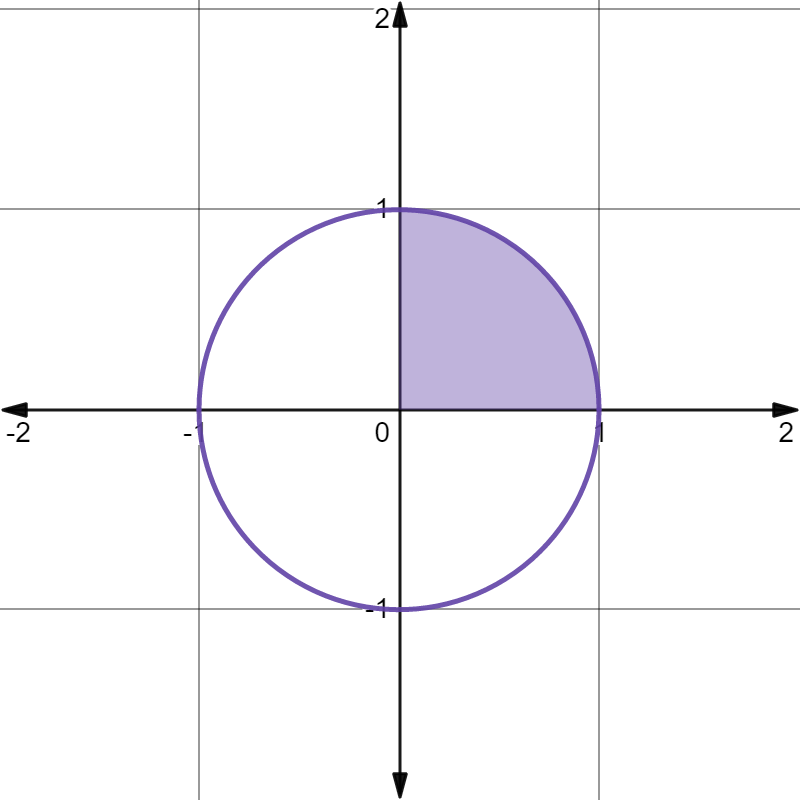
Graph of a full circle — The circle is $x^2+y^2=r^2,r=1$. The shaded region represents $\int^1_0{\sqrt{1-x^2}dx}$, which is $\frac{\pi}{4}$

Therefore, taking the integral of 1/4 the circle, then multiplying by 4 is the area of the circle, which is equal to π!

$$4\int^1_0{\sqrt{1-x^2}dx}=\pi$$

Circumference of the Universe

The circumference of the Observable Universe is a great novelty problem to demonstrate the precision of π. According to NASA at JPL, 40 digits of π is precise enough to calculate it within the radius of a single hydrogen atom. JPL themselves only use 15 digits.

Putting it on a business card

As of writing this page, my very limited programming experience is in C++. Python looks like an awesome language, and its beautiful syntax is much more conducive to printing on a business card. 🙂 Using one of Python’s many libraries to take the integral would be infinitely easier and more efficient, but using the Fundamental Theorem of Calculus (a Riemann sum) to approximate π is way cooler. To be clear, this is an extremely inefficient (but badass) way to calculate pi; I ran it for 10 billion iterations and couldn’t even get close to 15 digits.

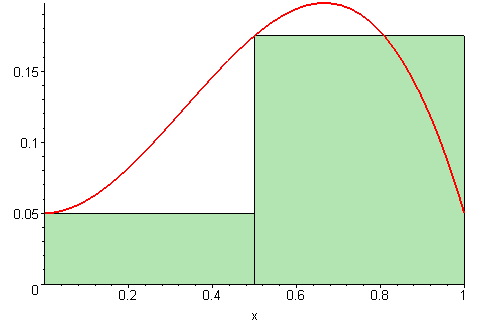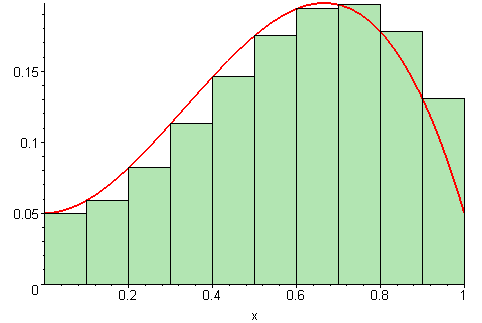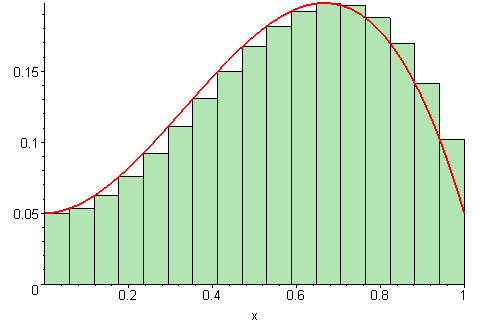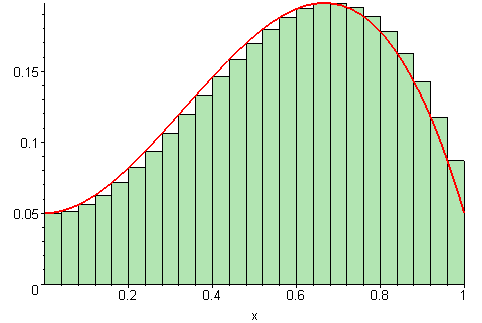
Animated Riemann sum graph — A Riemann sum looks like this, with the rectangles becoming infinitely narrow. An integral is just the area of all the rectangles added together [1]

In my case, the integral can be represented as this Riemann sum:

$$\pi=4\int^1_0{\sqrt{1-x^2}dx}=4\lim\limits_{n\to \infty}\sum_{i=1}^n\sqrt{1-(\frac{i}{n})^2}\cdot\frac{1}{n}$$

To approximate π in a computer program, the limit can be dropped and n replaced with a reasonably large number. This is how I translated it into python:

import math
n = 1000000
dx = (1/n)
s = 0
for i in range(1, n):
    x_i = (math.sqrt(1-math.pow((i/n),2))*dx)
    s += x_i
print("Approximate pi:", '{:0.6}'.format(4*s))
d = 8.8E26 # Observable universe, meters
print("Circumference of the Universe:", '{:0.1e}'.format(d*4*s,1), "m")
## Accurate to (8.4E-5)%, or 840 parts per billion!

Output:

Approximate pi: 3.14159
Circumference of the Universe: 2.8e+27 m

[1] “File:Riemann sum (leftbox).gif” by 09glasgow09 is licensed with CC BY-SA 3.0. To view a copy of this license, visit https://creativecommons.org/licenses/by-sa/3.0

Last modified: 2021-09-10