SV Control: Desaturating Reaction Wheels in the Satellite Simulator

Background: my professor for Space Vehicle control (Dr. Eric Swenson) wrote an incredible satellite dynamics simulator with a PID controller in MATLAB. Assignments for the class provided a specific end condition of the vehicle, and we wrote code that controls the simulator. A big part of it was representing the rotation from initial to final attitude; I liked to use dot/cross products, Euler axis/angle, DCMs, and quaternions depending on the situation. Below is my favorite problem out of all the assignments

Objective

As shown below, the objective for this problem is to point the SV body axes at \(\langle 1,1,1 \rangle\frac{1}{\sqrt 3} \) in the inertial frame, and use the thrusters to dump angular momentum accumulated from a disturbance torque once the reaction wheels saturate at 3500 rpm.

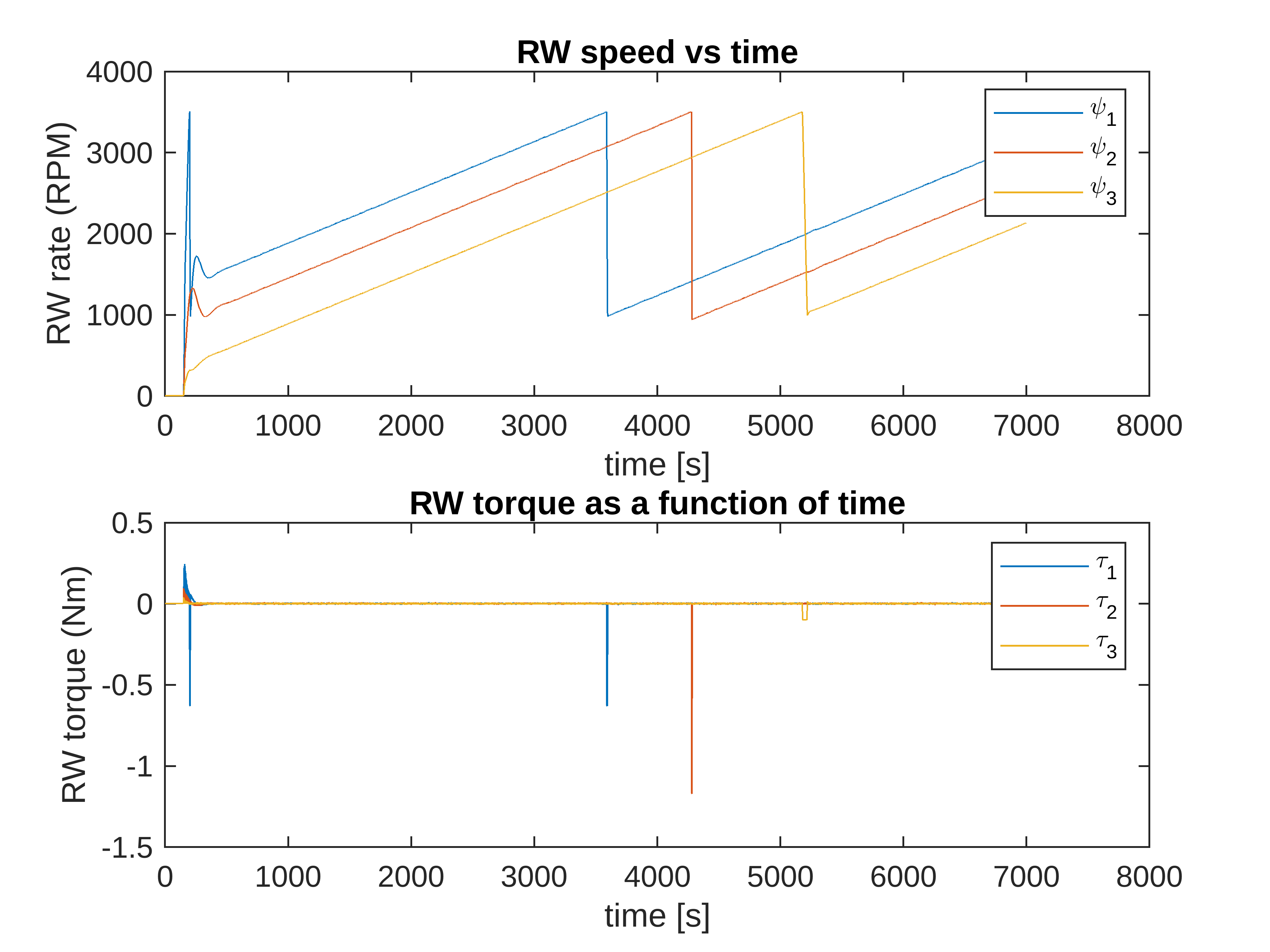
plot of reaction wheel speed vs time — Reaction wheel RPM drops from 3500 to 1000 during desaturation, while thrusters hold the vehicle at a constant attitude

NOTE: \(\tau_3\) is significantly smaller than the other torques because the 3-axis has a much lower mass moment of inertia.

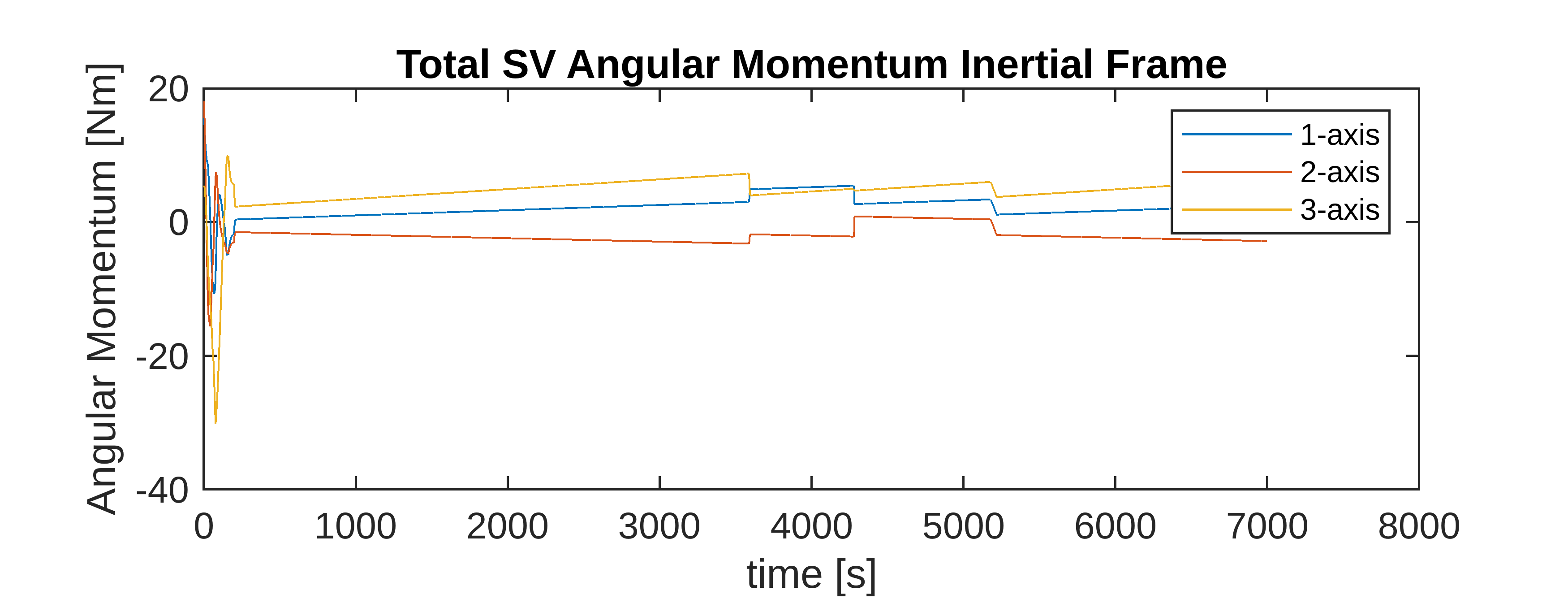
plot of SV angular momentum vs time — Angular momentum is constantly increasing from the disturbance torque; desaturation reduces it to the amount stored by the reaction wheels at 1000 RPM

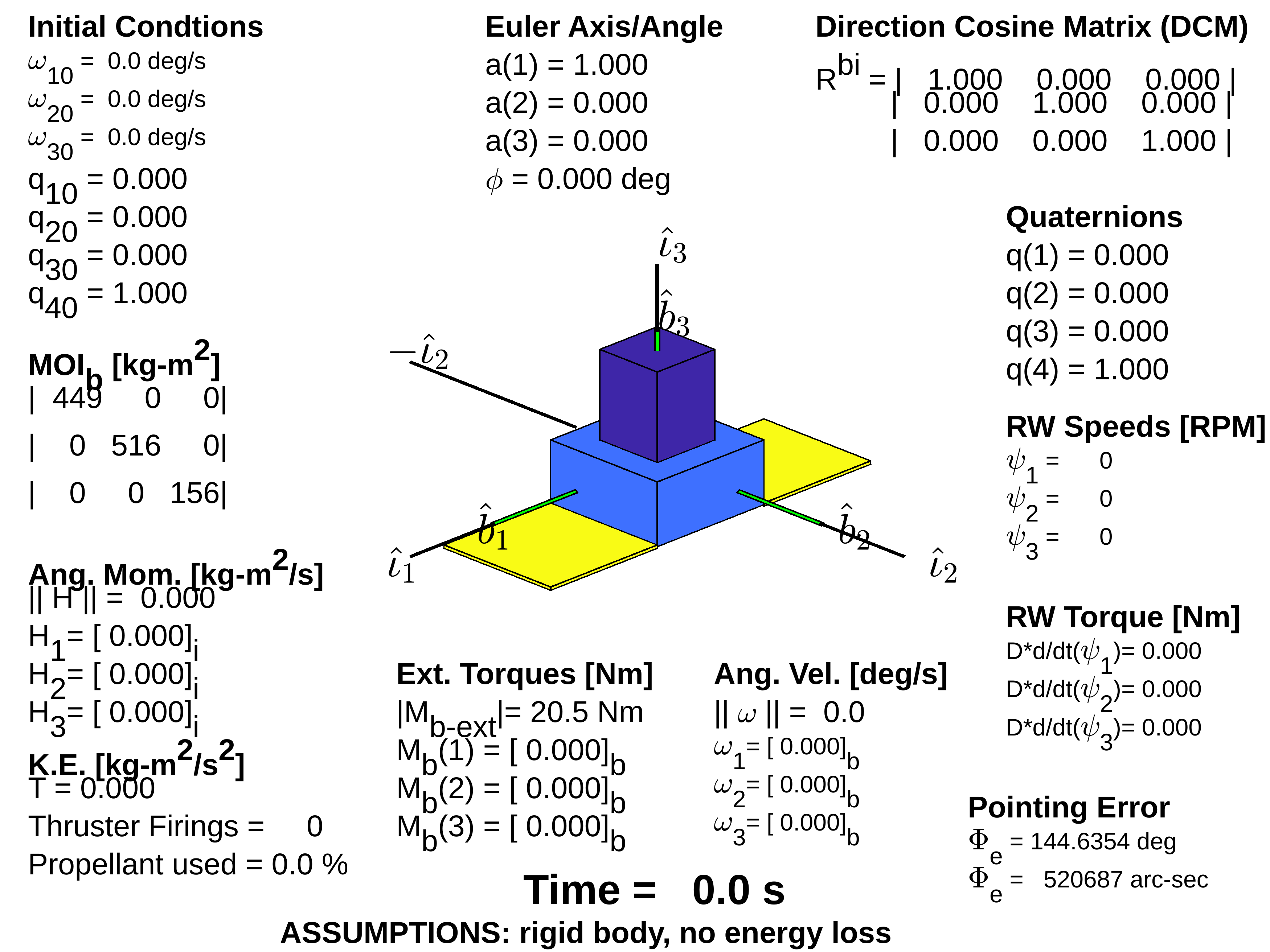
initial attitude of satellite with parameters — Initial attitude of space vehicle \(\langle 1,1,1 \rangle_i \)

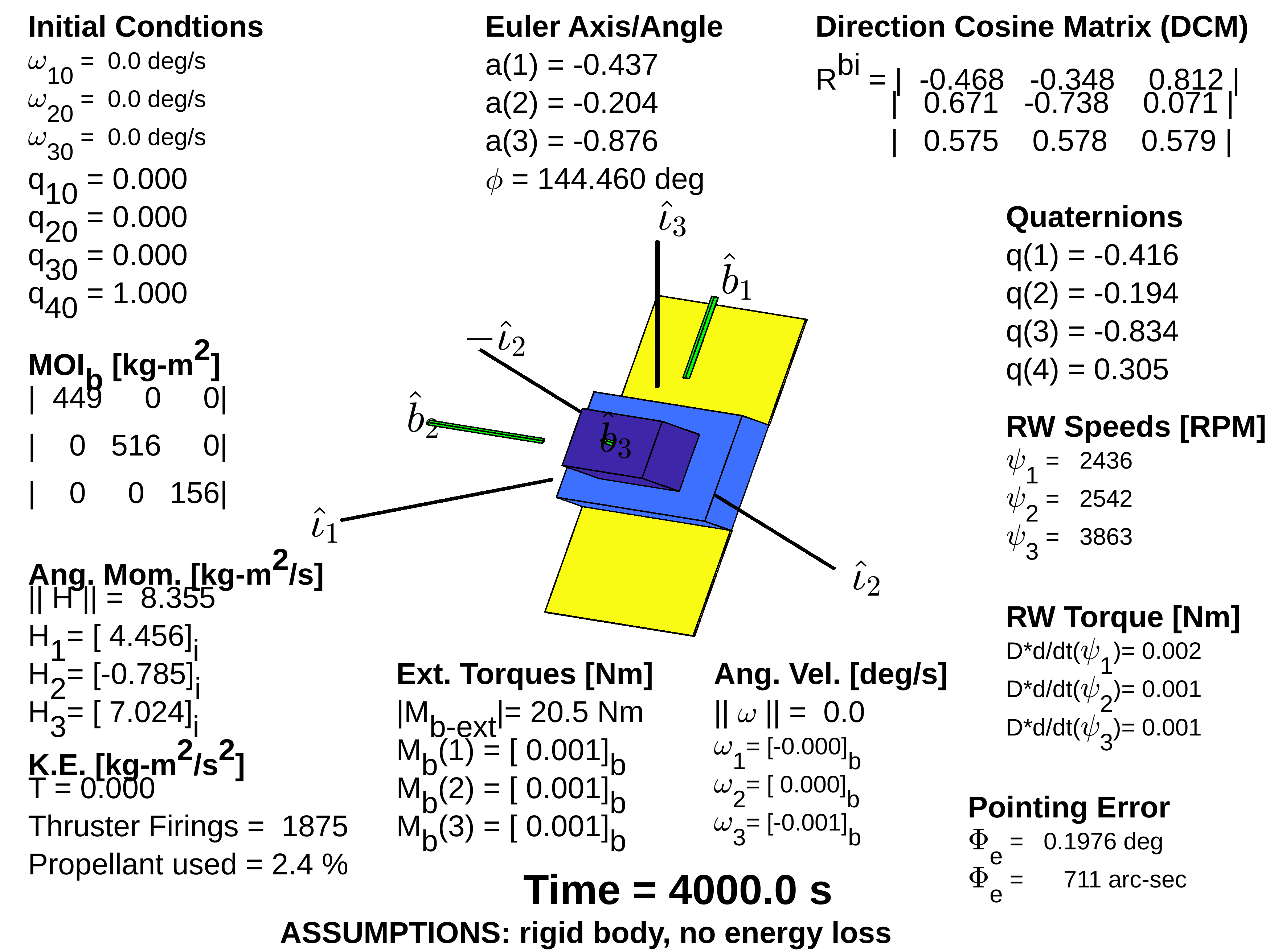
final attitude of satellite with parameters — Final attitude of space vehicle \(\frac{1}{\sqrt 3}\langle 1,1,1 \rangle_i \)

Interesting Code Snippets

Commanded attitude

Computes the final attitude by crossing the body axes into the target vector, converting to euler angle/axis, then a direction cosine matrix multiplied by an extra 3-rotation, then a quaternion, which ultimately becomes the transmuted quaternion matrix for simulator input.

%% FINAL COMMANDED ATTITUDE via a rotation matrix and quaternions
target = [ 1 1 1 ]/sqrt(3);
b3_i= [0 0 1];

% Quaternion pointed at target
a1 = cross(b3_i, target)';
a1=a1/norm(a1);
phi = acos(dot(b3_i, target)/(norm(b3_i)*norm(target)));
[~,~, R_target, ~] = Q2R([a1*sin(phi/2); cos(phi/2)]);

% Additional 3-rotation
theta_1 = deg2rad(220);
R_3_1 = [ cos(theta_1)   sin(theta_1)     0  ; 
         -sin(theta_1)   cos(theta_1)     0   ;
              0               0           1];
R_bi = R_3_1*R_target;

% Final commanded attitude
[~,~,q_commanded] = R2Q(R_bi);
disp(sprintf('Commanded quaternion = [ %8.6f   %8.6f   %8.6f   %8.6f ]',q_commanded))

Desaturate

The desaturation code runs once per cycle of the outer control loop. It checks whether the wheels are saturated or finished desaturating, then sets a global boolean to turn the next function on/off. If on, it uses the equation \(\dot\psi=\frac \tau D\) to determine the wheel deceleration rate that produces an internal torque equal and opposite the external torque produced by the thrusters; where \(\dot\psi\) is angular accerlation, \(D\) is the wheel’s mass moment of inertia, and \(\tau\) is the external torque. The angular acceleration (\(\dot\psi\)) is in the direction opposite the wheel’s current rotation. This process repeats for each control timestep until wheel RPM drops below 1000.

for ctr = 1 : 3 % Enforce RW torque and angular velocity constraints
if abs(psi(ctr)) > 3500*2*pi/60 && desaturate(ctr) == false
    desaturate(ctr) = true;
end

if abs(psi(ctr)) < 1000*2*pi/60 && desaturate(ctr) == true
    desaturate(ctr) = false;
end
    
if desaturate(ctr) == true
        %disp(strcat('RW #',num2str(ctr), ', above 3500 rpm at time=',num2str(start_time)) );
        thruster_torque(ctr) = -2*nominal_thrust*moment_arm(ctr);
        thrusters_fired_ctr = thrusters_fired_ctr + 2*sum(abs(thruster_torque)); % count # times the thrusters are fired
        psi_dot(ctr) = sign(psi(ctr))*thruster_torque(ctr)/D_rotor;
    M_b_ext = M_b_ext + thruster_torque; % add tot total external torque on SV
end
end

Last modified: 2023-11-20